Example 2.5

In what follows, we will implement transformation methods for sampling continuous distributions.

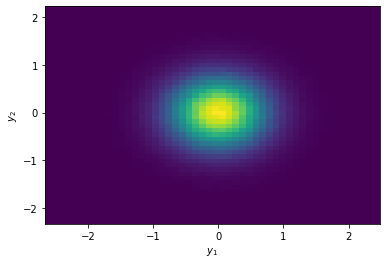
Example 2.5. Let us implement the transformation method where

\[\begin{align*} X_1 &\sim \text{Exp}\left(\frac{1}{2}\right), \\ X_2 &\sim \text{Unif}(-\pi, \pi), \end{align*}\]

and

\[\begin{align*} Y_1 &= \sqrt{X_1} \cos X_2 \\ Y_2 &= \sqrt{X_1} \sin X_2. \end{align*}\]

import numpy as np
import matplotlib.pyplot as plt

rng = np.random.default_rng(123)

N = 1000000
x_1 = rng.exponential(1/2, N)
x_2 = rng.uniform(-np.pi, np.pi, N)

y_1 = np.sqrt(x_1) * np.cos(x_2)
y_2 = np.sqrt(x_1) * np.sin(x_2)

# plot 2d histogram of y_1 and y_2
plt.hist2d(y_1, y_2, bins=50)
plt.xlabel('$y_1$')
plt.ylabel('$y_2$')
plt.show()