The Kalman filter#
The model below is taken from the paper, Section 5.3 with simplifications.
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.default_rng(1234)
# define the linear system for object tracking
# x = [x, y, vx, vy]
T = 1000
x = np.zeros((4, T))
x[:, 0] = np.zeros(4)
k = 0.04
# A is a matrix 4x4 matris
# [I_2, kappa*I_2;
# 0_2, 0.99 * I_2]
A = np.block([
[np.eye(2), k * np.eye(2)],
[np.zeros((2, 2)), 0.99 * np.eye(2)]
])
Q = np.block([
[k**3 / 3 * np.eye(2), k**2 / 2 * np.eye(2)],
[k**2 / 2 * np.eye(2), k * np.eye(2)]
])
H = np.array([[1.0, 0.0, 0.0, 0.0], [0.0, 1.0, 0.0, 0.0]])
print(H)
R = 1 * np.array([[1, 0.0], [0.0, 1]])
y = np.zeros((2, T))
for t in range(1, T):
x[:, t] = A.dot(x[:, t-1]) + rng.multivariate_normal(np.zeros(4), Q)
y[:, t] = H.dot(x[:, t]) + rng.multivariate_normal(np.zeros(2), R)
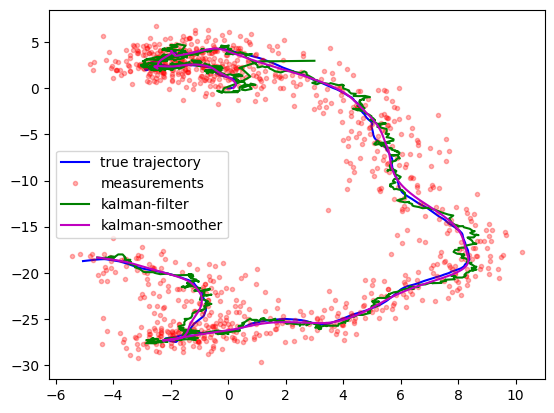
plt.plot(x[0, :], x[1, :], 'b-')
plt.plot(y[0, :], y[1, :], 'r.', alpha=0.3)
plt.legend(['true trajectory', 'measurements'])
[[1. 0. 0. 0.]
[0. 1. 0. 0.]]
<matplotlib.legend.Legend at 0x125a349a0>
mu = np.zeros((4, T))
V = np.zeros((4, 4, T))
mu[:, 0] = np.ones(4) * 3
V[:, :, 0] = 10 * np.eye(4)
mu_pred = np.zeros((4, T))
V_pred = np.zeros((4, 4, T))
for t in range(1, T):
mu_pred[:, t] = A.dot(mu[:, t-1])
V_pred[:, :, t] = A.dot(V[:, :, t-1]).dot(A.T) + Q
S = H.dot(V_pred[:, :, t]).dot(H.T) + R
K = V_pred[:, :, t].dot(H.T).dot(np.linalg.inv(S))
mu[:, t] = mu_pred[:, t] + K.dot(y[:, t] - H.dot(mu_pred[:, t]))
V[:, :, t] = V_pred[:, :, t] - K.dot(H).dot(V_pred[:, :, t])
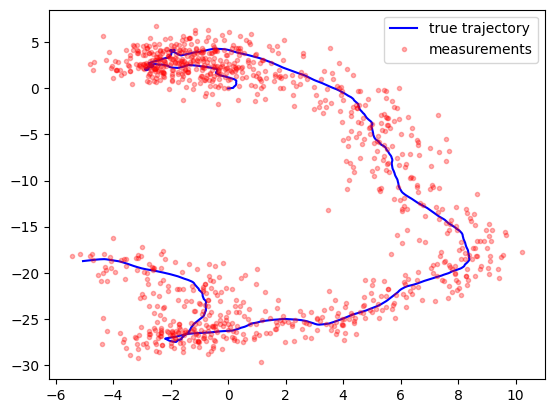
plt.plot(x[0, :], x[1, :], 'b-')
plt.plot(y[0, :], y[1, :], 'r.', alpha=0.3)
plt.plot(mu[0, :], mu[1, :], 'g-')
plt.legend(['true trajectory', 'measurements', 'kalman-filter'])
plt.show()
# Kalman smoother
mu_smooth = np.zeros((4, T))
V_smooth = np.zeros((4, 4, T))
mu_smooth[:, -1] = mu[:, -1]
V_smooth[:, :, -1] = V[:, :, -1]
for t in range(T-2, -1, -1):
J = V[:, :, t].dot(A.T).dot(np.linalg.inv(V_pred[:, :, t+1]))
mu_smooth[:, t] = mu[:, t] + J.dot(mu_smooth[:, t+1] - mu_pred[:, t+1])
V_smooth[:, :, t] = V[:, :, t] + (J.dot(V_smooth[:, :, t+1] - V_pred[:, :, t+1])).dot(J.T)
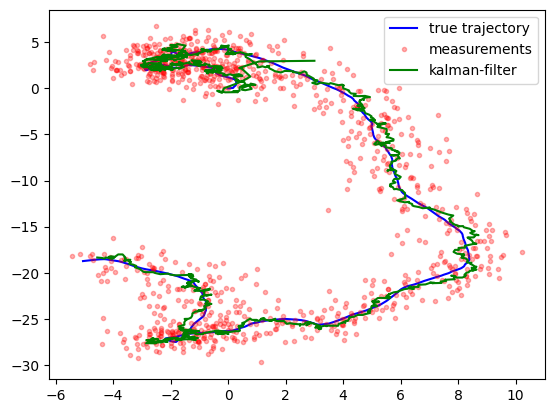
plt.plot(x[0, :], x[1, :], 'b-')
plt.plot(y[0, :], y[1, :], 'r.', alpha=0.3)
plt.plot(mu[0, :], mu[1, :], 'g-')
plt.plot(mu_smooth[0, :], mu_smooth[1, :], 'm-')
plt.legend(['true trajectory', 'measurements', 'kalman-filter', 'kalman-smoother'])
plt.show()